1. Definition of an ellipse:
"The set of all points such that the sum of the distance from the two points is a constant."
-Mrs. Kirch
.
2. The image above provides the equation to an ellipse. An ellipse will be horizontal (fat) or vertical (skinny) based on the bigger denominator. The left ellipse will be "fat" because the bigger number lies under the x^2 denominator; meanwhile, the right ellipse is "skinny" since the bigger denominator is under the y^2. Their order does not necessarily matter; instead, the graph is based on the bigger denominator. The main kepy points to find for an ellipse would be center, foci, major axis, minor axis, vertices, co-vertices, and eccentricity.
 |
| http://www.teacherschoice.com.au/images/ellipse_types.gif |
If you are given the standard equation, all you have to do is complete the square before you can continue solving the puzzle. Remember, the standard form has to equal to 1 and must be added (just as the algebraic equation above shows).
X always goes with "h" and Y always goes with "k", so base the center on the given equation. For example, if the equation was (x-2)^2/25 + (y+2)^2/64=1, then the center would simply be (2,-2). Given this information, you would know that the "y" has the bigger denominator and when graphed, the major axis would be x=2 and that only means the minor axis will be the other value, which will be y=-2. When these two lines are graphed, the major will be a solid line perpendicular to the dotted minor line. To find the vertices and co-vertices, keep in mind that the numbers will repeat based on the major and minor axis. In this case, x=2 for the major axis, the vertices will be (2, #) and (2, #).
Given that the center, the vertices, and the foci all have the similar repeating value, you can fill in the foci as (2, #) and (2, #). Go back the co-vertices and since it is based on the minor axis, you know that the repeating number will be (#, -2) and (#, -2). The "a" and "b" values help determine the remaining values for the vertices and co-vertices points. The "a" and "b" are the square roots from the the starndard equation. To find the foci, use the equation a^2-b^2=c^2.
Since most of the key points are based on the center, add the foci to the center, or the missing (non-repeating) value. You can find the eccentricity by dividing c over a. Since it's an ellipse, the
eccentricity should be between 0 and 1.
 |
| http://www.mathwarehouse.com/ellipse/images/eccentricity_of_ellipse.gif |
Take a look at the graph from this website to get an idea about an ellipse's eccentricity:
Click Here!
Notice how the picture on the left has an eccentricity of .8 (less than 1, yet close)
When graphing an ellipse, remember which lines are solid vs. which ones are dotted (see previous paragraph). Also, the vertices and the co-vertices will be perpendicula to each other and both will meet at the center. The vertices should be equidistant from the center on both sides and so should the co-vertices. The foci help determine the shape of the ellipse and are fairly close to the vertices. In fact, the closer the foci are to each other, the more circular the ellipse will be (vice versa).
 |
| http://t0.gstatic.com/images?q=tbn:ANd9GcScIq5UAbf3gnoaNjUdn5xmD4DCdO4eFKoo21Npaa6hTStyqLocWw:decodedpregnancy.com/assets/A03_Conic_Sections.jpg |
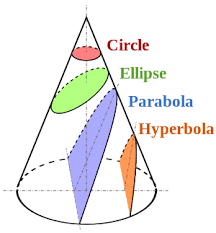
Want to know more about conics? Check this out!
3. Real World Application:
Ellipses are mostly since in our very own solar system and all around us, of course. The comets, planets, and moons all orbit the sun through their very own ellipse shape. As you can see, those closer to the sun have smaller ellipses; meanwhile, those farter apart have a bigger ellipse. "Because the Sun is at the focus, not the center, of the ellipse, the planet moves closer to and further away from the Sun every orbit" (http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html)
 |
| http://i1.ytimg.com/vi/VjQZ5QA-tNg/hqdefault.jpg |
A patient will be placed right before the machine at the precise distance from the focus point and the shock wave generator. Notice how the picture on the right shows the kidney stones in one focus point while the other focus point will be at the shock. A cushion surrounds the ellipsoid, so that the water within in provides a safe transmission between the shock waves that pass through one's body. In other words, the waves that generate from one focus point to the other focus point, which would be the kidney stone. The stones then shatter and it is easy for a patient to get rid of the stones without the need for surgery, but also achieves without much risks.
4. Works Cited: