How do the graphs of sine and cosine relate to each of the others? Emphasize asymptotes in your response.
Tangent:
Sine and cosine are always two of the main trig functions. So how do both of them relate to the tangen graphst? First, let's remember that the trig ratio for tangent is sin/cos or (y/x). As you may remember, sine is positive in the 1st and 2nd quadrant, cosine in the 1st and 4th quadrant, and tangent in the 1st and 3rd quadrant. Meanwhile, sine is negative in the 3rd and 4th, cosine in the 2nd and 3rd, and tangent in the 2nd and 4th. Therefore, let's say we want to find the answer to tangent, we need to divide sine over cosine first and the sign of those trig functions will depend on the quadrant they lie. If we look at the 2nd quadrant, sine is positive and cosine is not, so a positive divided by negative will give us a negative answer. Do you see it now? The answer is negative in the 2nd quadrant and tangent is also negative in second quadrant. In the first quadrant, both are positive (sine and cosine), so then tangent is also positive. For the 3rd quadrant, both sine and cosine are negative, meaning that the answer will be positive (tangent is positive in the 3rd quadrant.) Lastly, in the 4th quadrant, sine is negative, but cosine is positive; nevertheless, the answer is negative, which means that tangent is also negative. Tangent will continue to go uphill based on these values
As for the asympotoes, tangent also derives it's distance between the asymptotes from sine and cosine. If tangent= sine/cos, the only way to get an asymptote (undefined ratio) is to let cos(x)=0 (denominator 0= undefined). According to the unit circle, the two values that give is cosine (x) as 0 would be at 
/2 and at 3

/2. Of course, the aysmptotes do not end there because they will continue to go on forever, never touching the asymptoes; yet, sine and cosine will be there to help us find tangent.
Cotangent:
Cotangent is related to sine and cosine is a very similar way as it is related to tangent. The difference between the ratios is that now it's the reciprocal and cotangent: cosine/sine. Regardless of that, the signs for each trig function remain the same in given any quadrant. For example, in quadrant 1, cosine (+)/ sine (+) will give us a positive answer, which is similar to cotangent being positive in the 1st quadrant as well. In the 2nd quadrant, cos (-)/ sine (+), will lead to a negative number very much similar to cotangent being negative in the 2nd quadrant. Keep in mind that cotangent is positive in the 3rd quadrant, so when we divide cos (-)/ sin(-), then we also get a positive answer. Then for the last quadrant, cos(+)/ sin (-) give us a negative answer, which is what cotangent is in the 4th quadrant.
Similar to tangent, the denominator for cotangent also need to be 0 in order to get an asymptote. In other words, we need a value that has sin of theta equal to 0 since that would result in an undefined ratio. The values that have the y value as 0 would be 0 and 2

. Given the location of the asymptotes, we can start up for the 1st quadrant and then go down for the second quadrant, meaning that this time the graph will be downhill.
Secant:
Secant is much easier because it is the reciprocal of cosine, so that means that the ratio for secant is 1/cosine. Since cosine is the denominator, that means that the only want to get an aymptote would be to make cosine equal 0. So where does cosine equal 0? It equals 0 in

/2 and 3

/2 or at the 90* and 270*. This is also due to the fact that secant shares the same positive and negative values as cosine since they are reciprocal as I previously mentioned. Just so you can see it in action, let me show you an example. In the 2nd quadrant, cosine is negative so if we divide 1 (+) by cosine (-), then we get a negative answer similar to secant in the 2nd quadrant. The same method would be applied to secant as it can be applied to cosine.
Cosecant:
Just as cotangent was similar to tangent, cosencant will be similar to secant. We must first understand that cosecant is the reciprocal of sine, so the ratio would be 1/sin. This means that in order to get the asymptotes, sine (denominator) would have to be 0 to give us an undefined ratio. In order to get sine to equal 0, the values for the asymptote would have to be 0 and 2

. Also, let us not forget that cosecant will also share the similar sign values as sine because they are both positive in the 1st and 2nd quadrant, but negative in the 3rd and the 4th quadrant. Also, both will continue to have many, many asymptotes even though we tend to only show one period.
References:
SSS Packet- Unit T
Demos Packet
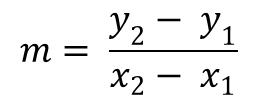



 /2 and at 3
/2 and at 3




