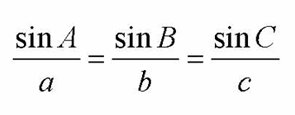BQ #7: Explain in detail where the formula for the different quotient comes from now that you know! Include all appropriate terminology (secant line, tangent line, h/delta x, etc).

We have known about the difference quotient for a long time now; in fact, it is often included in our tests. However, we really didn't know where it came from until we reached the last unit- Unit V! So let's take a closer look at how the difference quotient is derived.
Based on the first few concepts, we know that the difference quotient is only a part of the process when trying to find the derivative (the slope of tangent lines).

http://t3.gstatic.com/images?q=tbn:ANd9GcQx-jY-1cjcu_PSC9gGtoDW4qMYafVwaqWw8Qt5qV_gQpIKlz5w:cis.stvincent.edu/carlsond/ma109/DifferenceQuotient_images/IMG0470.JPG

Notice that the image on the left shows us two  main points. The first point is [x, f(x)]because the first value on our scale was "x". Since the first value under the x-axis is "x" that means that the value for y in that point is f(x).  There is another point, but does not have exact digits either. Therefore, we simply add the "h" (the distance between the two points) to the already known "x", so we can get "x+h". Then as we did before, the y-axis will be f of the x-axis, which turns out to be f(x+h).

http://t2.gstatic.com/images?q=tbn:ANd9GcSmctLWns4VWjJOvK672RQnfSPeu-73rvYghAvuGT_HhHTEhVRY3w:education-portal.com/cimages/multimages/16/Slope_formula_2.png

We continue to find the difference quotient by using the slope formula as shown above. After plugging in the values based on the slope formula we get [ f(x+h)-f(x)/ x+h-x]. Since the "x" in the denominator cancel out, we only have to simplify it to get [f(x+h) -f(x)/ h]....the difference quotient!!
Like I mentioned before, the difference quotient can be used to find the slope of a tangent line, which only touches the function once. We do not have to rely on the secant line because it touches the function twice. As a matter of fact, the reason why we try to find the limit as h approaches 0 is because we want "h" to be as close as possible to 0 so that both points can meet at one point instead of two like the secant line).

BQ #6- Unit U

What is continuity? What is discontinuity?

A continuity is basically a predictable graph  or a continuous graph.  A continuity is also described as a graph that "has no breaks, no holes, and no jumps". Another way you can identify a continuity is by drawing it without lifting  your pencil from the paper and makes a goof bridge. We are more familiar with continuities as we dealt with them in parabolas, linear graphs, etc. Meanwhile, discontinuities are the opposite of continuities since they do have holes, jumps, and breaks. Discontinuity graphs are categorized into two different "families". The two families are removable discontinuities and non- removable discontinuities. In removable discontinuities, the one example would be point discontinuities, or a hole. Non-removable discontinuities have three different examples: jump discontinuities, oscillating behavior, and infinite discontinuity. Jump discontinuities are graphs that have an open and closed circle, but do not connect. An oscillating behavior is a graph that looks sine curve, but is very wiggly. An infinite discontinuity is also known as unbounded behavior because it occurs where there is a vertical asymptote.

Removable Discontinuity:

Point Discontinuities

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif

Non-Removable Discontinuities

Jump Discontinuity

http://upload.wikimedia.org/wikipedia/commons/thumb/9/92/Jump_discontinuity_cadlag.svg/264px-Jump_discontinuity_cadlag.svg.png

Oscillating Behavior

https://encrypted-tbn3.gstatic.com/images?q=tbn:ANd9GcRGKnu-whU8KA1HjLrbu6pgV9JW_727lNXa-Eu-3sTzcp_zGqukDg

Infinite Behavior

https://encrypted-tbn2.gstatic.com/images?q=tbn:ANd9GcRp9ghtAEQLeV_IInaJpdPzTWbn-xansC05qQdrQ_6jz_yURt2TQQ

What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is "the intended height of a function". As for the values, it is the actual height of a graph. Keep in mind that a graph is continuous when the limit and the value are the same and we have no discontinuity. So now let's go back, where does a limit exist/ not exists?
A limit exists in any point within a continuous function and also exists in a hole because the graph still intended to reach a certain height. As for the value, the random point above would be the actual value since it is the actual height of the function (dark circle).

Analogy of why the limit still exists in a hole:

Two people are driving to a restaurant from two different routes. Once they get there, they noticed that the restaurant burned down. Despite the fact that they did not go inside the restaurant, the two different people still reached the intended destination- the restaurant.

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfi

However, a limit will fail to exists in non-removable discontinuities, such as jump, oscillating, and infinite behaviors. The reason why a limit would not exist in a jump discontinuity is because there are different left and right limits. Also, the value and the jump discontinuity in jump discontinuities are different. When looking for the values, the value of a jump discontinuity would be the dark or closed circle. A limit will not exist in an oscillating graph because there are too many values within the "wiggly" graph that it is difficult to pinpoint one single value or limit. The last discontinuity in which a limit does not exist would be in infinite behavior graphs. This usually happens when we have a vertical asymptote, which would lead into unbounded behavior graphs. We will forever more approach infinity, which means we cannot find a specific numerical value.

How do we evaluate limits numerically, graphically, and algebraically? 
One of the ways to evaluate limits would be by using a table. We take the limit and add or subtract (1/10) to it.(three for the left and three for the right). Those two values would be the end points of the table and those f(x) values would approach the limit. 
The other way we can evaluate limits would be graphically. When we find values to our table, we can simply plug the function into the "y=" sceen and trace them. There are times when the limits are graphed and in those cases, it would be easier to trace the graph with our own fingers. If out fingers meet then the limit does exist, but it is doesn't then the limit does not exist. 
Lastly, we can also find the limits algebraically. We can evaluate algebraically with direct substitution, factoring out, and finding the conjugate. We always want to start solving with direct substitution, which is basically substituting the x value that we are approaching into the function. You can will be done with the problem if you get a # (or fraction), 0/#, #/0, or 0/0 (indeterminate). If you do get indeterminate, then use the next methods. When we factor out the function we should be able to cancel something out (removable) that would result in a simply number which we can directly substitute back into the function. The other method would be rationalizing/ conjugate and it is usually used when we have a radical and cannot factor out anything. We follow by multiplying by the conjugate of the portion that has a radical. We foil the conjugate and leave the non-conjugates alone. Again, we should be able to substitute once we canceled something else.

References

http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfi

https://encrypted-tbn2.gstatic.com/images?q=tbn:ANd9GcRp9ghtAEQLeV_IInaJpdPzTWbn-xansC05qQdrQ_6jz_yURt2TQQ

https://encrypted-tbn3.gstatic.com/images?q=tbn:ANd9GcRGKnu-whU8KA1HjLrbu6pgV9JW_727lNXa-Eu-3sTzcp_zGqukDg
http://upload.wikimedia.org/wikipedia/commons/thumb/9/92/Jump_discontinuity_cadlag.svg/264px-Jump_discontinuity_cadlag.svg.png
SSS Packet

BQ #4: Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill?

Again, we are going to go back to the Unit Circle and as the unit circle tells us, the trig ratio for tan=y/x and cot= x/y since it's the reciprocal of tangent. Another way we can see these ratios is tan=sin/cos and cot= cos/sin.  Look that the paragraphs and the images for more details. With this in mind,  cos would need to equal 0 for tangent and sin would need to equal 0 for cotagent in order to find our asymptotes since they are undefined ratios.

For tangent, Cos would be 0 at 90* (pi/2) and 270* (3pi/2). Before we graph, also remember that the pattern for tangent will be  + - + -. Now, let's label our graph based on the quadrants and their pattern, but highlight where the asymptotes will lie on.
You can see that based on the asymptotes, you need to draw your graph within those two quadrant. It lies on the second quadrant , which is negative and then in quadrant three, which is positive. When you connect those two, your graph will go uphill.

Now as for cotangent, you also need to remember that in order to get an asymptote, sin will need to equal 0. Based on the unit circle, sin=0 at 0* (0pi) and 180* (pi). The pattern for cotangent is the same as it is for tangent ( +-+-). Once we label our graph and highlight the asymptotes, we need to look at the quadrants that lie within those asymptotes. We land on the first quadrant, which is positive and then in the second quadrant, which will be negative. Once we connect these pieces together, we get a downhill graph.

BQ#3 – Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

Tangent: Sine and cosine are always two of the main trig functions. So how do both of them relate to the tangen graphst? First, let's remember that the trig ratio for tangent is sin/cos or (y/x). As you may remember, sine is positive in the 1st and 2nd quadrant, cosine in the 1st and 4th quadrant, and tangent in the 1st and 3rd quadrant. Meanwhile, sine is negative in the 3rd and 4th, cosine in the 2nd and 3rd, and tangent in the 2nd and 4th. Therefore, let's say we want to find the answer to tangent, we need to divide sine over cosine first and the sign of those trig functions will depend on the quadrant they lie. If we look at the 2nd quadrant, sine is positive and cosine is not, so a positive divided by negative will give us a negative answer. Do you see it now? The answer is negative in the 2nd quadrant and tangent is also negative in second quadrant. In the first quadrant, both are positive (sine and cosine), so then tangent is also positive. For the 3rd quadrant, both sine and cosine are negative, meaning that the answer will be positive (tangent is positive in the 3rd quadrant.) Lastly, in the 4th quadrant, sine is negative, but cosine is positive; nevertheless, the answer is negative, which means that tangent is also negative. Tangent will continue to go uphill based on these values

As for the asympotoes, tangent also derives it's distance between the asymptotes from sine and cosine. If tangent= sine/cos, the only way to get an asymptote (undefined ratio) is to let cos(x)=0 (denominator 0= undefined). According to the unit circle, the two values that give is cosine (x) as 0 would be at /2 and at 3/2.  Of course, the aysmptotes do not end there because they will continue to go on forever, never touching the asymptoes; yet, sine and cosine will be there to help us find tangent.

Cotangent:

Cotangent is related to sine and cosine is a very similar way as it is related to tangent. The difference between the ratios is that now it's the reciprocal and cotangent: cosine/sine. Regardless of that, the signs for each trig function remain the same in given any quadrant. For example, in quadrant 1, cosine (+)/ sine (+) will give us a positive answer, which is similar to cotangent being positive in the 1st quadrant as well. In the 2nd quadrant, cos (-)/ sine (+), will lead to a negative number very much similar to cotangent being negative in the 2nd quadrant. Keep in mind that cotangent is positive in the 3rd quadrant, so when we divide cos (-)/ sin(-), then we also get a positive answer. Then for the last quadrant, cos(+)/ sin (-) give us a negative answer, which is what cotangent is in the 4th quadrant.

Similar to tangent, the denominator for cotangent also need to be 0 in order to get an asymptote. In other words, we need a value that has sin of theta equal to 0 since that would result in an undefined ratio. The values that have the y value as 0 would be 0 and 2. Given the location of the asymptotes, we can start up for the 1st quadrant and then go down for the second quadrant, meaning that this time the graph will be downhill.

Secant:

Secant is much easier because it is the reciprocal of cosine, so that means that the ratio for secant is 1/cosine. Since cosine is the denominator, that means that the only want to get an aymptote would be to make cosine equal 0. So where does cosine equal 0? It equals  0 in /2 and 3/2 or at the 90* and 270*. This is also due to the fact that secant shares the same positive and negative values as cosine since they are reciprocal as I previously mentioned. Just so you can see it in action, let me show you an example. In the 2nd quadrant, cosine is negative so if we divide 1 (+) by cosine (-), then we get a negative answer similar to secant in the 2nd quadrant. The same method would be applied to secant as it can be applied to cosine. 

Cosecant:

Just as cotangent was similar to tangent, cosencant will be similar to secant. We must first understand that cosecant is the reciprocal of sine, so the ratio would be 1/sin. This means that in order to get the asymptotes, sine (denominator) would have to be 0 to give us an undefined ratio. In order to get sine to equal 0, the values for the asymptote would have to be 0 and 2. Also, let us not forget that cosecant will also share the similar sign values as sine because they are both positive in the 1st and 2nd quadrant, but negative in the 3rd and the 4th quadrant. Also, both will continue to have many, many asymptotes even though we tend to only show one period.

References:
SSS Packet- Unit T
Demos Packet

BQ #5: Unit T: Concepts 1-3: Why do sine and cosine NOT have asymptotes, but the other four trig graphs do?

So in order to figure out why sine and cosine do not have asymptotoes, we need to understand what an asymptote is. It is basically an undefined ratio, or a ratio that is divided by 0. Keeping that in mind, let's look at the trig ratios once again:

https://precalculusnwr7.wikispaces.com/file/view/Data_table_for_math_wikispaces.JPG/317767144/384x311/Data_table_for_math_wikispaces.JPG

http://staff.argyll.epsb.ca/jreed/math30p/trigonometry/unitCircle.htm

Notice how the only trig ratios to not have "r" are sine and cosine and "r" represent 1 on the unit circle. So whatever you divide sine and cosine by, the denominator will be 1 and therefore, it will not be undefined (asymptote). An asymptote can only exist when the denominator is 0 in order to reach the undefined value. Meanwhile, the other four trig graphs do not have a 1 as a denominator, meaning that they could have a 0 as a denominator to make it undefined and thus an asymptote. In order words, cosecant and cotangent can have asymptotes if the "y" (denominator) is equal to 0. This would apply to secant and tangent is the x is  also equal to 0.

Reference:
https://precalculusnwr7.wikispaces.com/file/view/Data_table_for_math_wikispaces.JPG/317767144/384x311/Data_table_for_math_wikispaces.JPG

http://staff.argyll.epsb.ca/jreed/math30p/trigonometry/unitCircle.htm

SSS Packet Unit T

BQ #2: Unit T: Concept Intro: How do trig graphs relate to the Unit Circle?

How do the trig graphs relate to the unit circle?
The Unit circle relates to the trig functions because it helps describe where the positive and negative sections of the graph come from, so that we can derive the periods of each trig function in order to graph it. When you look at the graph below, notice how the sine (Blue) is positive, which is basically covering the 1st and 2nd quadrant because sine is positive there. Then, it continues to go down to reflect that sine is negative in the 3rd and the 4th quadrant. As for cosine (Green), the positive uphill tells us that cosine is positive in the 1st quadrant and then goes down because cosine is negative in the 2nd quadrant. The downhill also shows that cosine is negative in the 3rd quadrant since it is still negative. It finally goes back up because cosine is positive in the 4th quadrant. The tangent graph (Orange) also goes through the similar situation, but according to the ASTC pattern as well. So first the graph starts in the 1st quadrant because all trig functions are positive there and it becomes negative since tangent is negative in the 2nd quadrant. It finally goes back up to a positive position because tangent is positive in the 3rd quadrant and then goes back to negative in the 4th quadrant.

Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

Let's start by defining what a period is in order to understand how it relates to the graphs.
Period: The period for sine/cosecant and cosine/secant is 2 because it will take 4 quadrants (based on ASTC) to repeat the pattern (or one time to go through the cycle)

Sine is + + - -

http://geogebratube.com/student/m25914

Cosine is + - - +

http://geogebratube.com/student/m25914

Sine and Cosine may have an amplitude of 2, the period for Tangent and Cotangent is simply  because tangent has a pattern on +-+- (based on ASTC).  In other words, it has a positive and then a negative within the first two quadrants.

 Tangent + - + -

http://geogebratube.com/student/m25914

 Remember, a period is only how much it take to go through the cycle even though it is never-ending; in fact, periods can continue on forever, but we only want to look at one period in order to understand how it relates to the trig functions.


Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

Amplitudes are half the distance between the highest and lowest points on the graph. All we need to look at is the value of "a" to find it (Kirch). So why is it that sine and cosine have an amplitude, but not tangent? Well, going back to the unit circle, sine and cosine both have "r", which equal 1 in their trig ratios. Sine and cosine have a restriction because they cannot have a value greater than 1 or less than -1. In fact, this would result in a "no solution". However, tangent/cotangent do not have 1 and are not restricted to 1 and can have other values that do not have to be in between -1 and 1.

https://share.ehs.uen.org/taxonomy/term/300

References:
https://share.ehs.uen.org/taxonomy/term/300
http://geogebratube.com/student/m25914
Unit T SSS Packet

Reflection 1: Unit Q Verifying Trig Functions

          1. Verifying trig functions are not easy at first,  I won't lie. However,  I know one can easily verify functions by following a series of steps. To verify a trig function basically means to prove how one can derive the trig based on another trig function.  Our goal is to simply,  find the conjugate,  etc. in order to find the answer. It usually takes a while, but you can start looking at thw hints that you are given.
          2. I usually start by looking at the similarities I  my problem.  For example, if I know that one of the trig function is an identity that can the canceled with another, I will find a way to cancel it out with ratio identities. I also try to turn everything into sin and cos.  One of the most common process I use is finding the conjugate for concept 5. For other simpler concepts, I tend to separate them and then proceed to cancel.
          3. My first step tends to be to look at the problem for anything that I can cancel off. In reality,  most times I just try anything because I willw eventually find the answer.  Then, I go into factoring anything needed and sometimes by doing so,  I can replace it by a Pythagorean identity. Once I can use my identies, I can continue finding other things that can be canceled. Mainly,  do not over think something because the answer might just be in front of you. Good luck!

SP #7: Unit Q Concept 2: Finding all trig functions when given one trig function and quadrant

This SP7 was made in collaboration with Adrie. Please visit the other awesome posts on her blog by going here. 



What is this problem about?
This problem will go over the steps on how to all trig functions when given one trig function and a quadrant by using identities. We will also try to fund the trig functions using SOH-CAH-TOA to show that both methods can give us the same answers.


Identity Work (Unit Q Concept 2)

SOH-CAH-TOA Work (Unit O Concept 5)

Make sure you pay attention to the rationalization, because we can never have a radical as a denominator. Along with that, make sure to remember your identities, so you know why we plug the values in those numbers. Also, keep in mind that 

Pay close attention to the relationships because in the end, SOh-CAH-TOA and trig function identities both give us the same answer to all trig functions.

I/D #3: Unit Q: Pythagorean Identities

1. Where does sin²x + cos²x  = 1 come from?

http://i1.ytimg.com/vi/o-fAx_96lgw/maxresdefault.jpg

Well, let's start by defining this as the main Pythagorean Identity. So what is an identity? They are proven facts and formulas that are always true, so we can go ahead and manipulate the expressions and equations. The equation that we can manipulate (not redefine) is the Pythagorean Theorem because it  is also an identity that will help us help us derive sin^2x+cos^2x=1.
So let's back up a little. The Pythagorean Theorem is a^2+b^2=c^2. However, when referring to a unit circle, the Pythagorean Theorem is written as x^2+y^2= r^2.

http://www.contracosta.edu/legacycontent/math/Pythagoras.htm

This is how the Pythagorean Theorem is drawn on the unit circle, with r=1. So how do we get r^2 to equal 1? We simply do divide it all by r^2 (both sides)

x^2 + y^2 =r^2
                               >>>  (x/r)^2 + (y/r)^2 = 1    We cancelled off r^2
r^2     r^2   r^2

Now, take a closer look at the fraction and what do you see? Anything familiar, perhaps the ratio for cosine and sine on the unit circle?? Yes? Yes!
Based on one of previous units, we found out that the ratio for cosine is x/r and the ratio for sine is y/r. Notice how they are written the same way, except that they are both squared. So we can just replace the ratios by the trig function name. Therefore, we get: sin^2x+cos^2x=1
This helps prove the reason why the Pythagorean Theorem is an identity since it can be manipulates, but the facts and formula is always the same even though a little rearranged.
Let's actually prove that this works though. Since we are talking about the unit circle, we can use one of the "Magic 3" pairs from the Unit  Circle. Let's use 45 because it has different x and y values.
The ordered pair is :(√2/2)>>>> Substitute them in the equation:  (√2/2)² + (√2/2)² = 1. (√2/2)²
When we simplify it, we get (1/2) + (1/2)=1, so this helps us prove that then identity is true!

Now we can proceed to find the next two Pythagorean Identities:
We can first find the tangent derivation by dividing the main identity by cos^2/x.
sin^2x   +   cos^2x    =    1
                                                                >>  tan²x + 1 = sec²x.                         The cos^2x cancel to equal 1
cos^2/x       cos^2/x     cos^2/x                                Then we find the rest by using the ratio/reciprocal identities


It is very important to remember the ratio identities in order to make your life easier and know where we get our substitutions!

http://www.sosmath.com/CBB/viewtopic.php?t=41908

Now we can continue to find cotangent derivation by dividing everything by sin^2x
sin^2x   +   cos^2x    =    1
                                                                >>  cot ²x + 1 = csc²x                The sin^2x will cancel to equal 1
sin^2x         sin^2x       sin^2x                                 Then we find the rest by using the ratio/reciprocal identities


Inquiry Activity Reflection:
1. The connections that I see between Units N, O, P, and Q so far are that the unit circle and the trig functions will continue to reappear and help define most of the trig functions and anything that relates to it even though equations are always being rearranged. Also, I learn the significance of sin and cos because all trig functions eventually relate back the them. It is almost like the universal trig function. 
2. If I had to describe trigonometry in THREE words, they would be... interconnected, confusing,and mind-blowing. 

WPP #13 and 14: Unit P Concept 6 and 7: Law of Sines and Law of Cosines

Please see my WPP13-14, made in collaboration with Vanessa Morales, by visiting their blog here.  Also be sure to check out the other awesome posts on their blog

BQ#1: Unit P Concepts 1 and 4: Law of Sines, Area of an Oblique Triangle, and their Derivations

http://htmartin.myweb.uga.edu/6190/quickreview3a.html

1. The Law of Sines AAS or ASA
When we use trig function, we usually use them only with right triangles. All we have to remember if SOH -CAH- TOA or the Pythagorean Theorem. What if it is not a right triangle? Well, we can still use the trig function, to determine the Law of Sines. This way we can determine for non-right triangles.

Here it how we derive the Law of Sines:

Add cahttp://www.mathamazement.com/Lessons/Pre-Calculus/06_Additional-Topics-in-Trigonometry/law-of-sines.htmlption

This is a non-right triangle, but we can simply make it a right triangle by drawing a perpendicular line from <B.  Now we have two right triangles that we can work with.

http://www.mathamazement.com/Lessons/Pre-Calculus/06_Additional-Topics-in-Trigonometry/law-of-sines.html

When we drew the perpendicular line, we got two right triangles. The perpendicular line can be called "h".  Let's look at the relationships that the sides and angles have based on the trig function. When we do this we could get SinA=h/a and SinC=h/a (opposite.adjacent). Both equations have fractions, so to get ride of the fractions, we can , multiply by the denominator. Once we do that we get cSin A=h and aSin C=h. Since both equal "h" we can use the transitive property to get c Sin A= a Sin C. Lastly, divide both sides by "ac" to cancel off the c in one equation and a in the other.

Now we have Sin A/a= Sin C/c. However, the equation also includes SinB/b. Why don't we have it. Well, that's because we cut <B with a perpendicular. However, if we can drawn the perpendicular line from another angle, such as <A, then we could get Sin B/b.
We follow the same process and we get Sin C= h/b and Sin B=h/c.  Use the transitive property and divide by "bc" and we can also get Sin B=b. Let's put it all together and we get.

                    

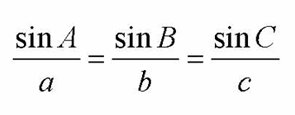http://www.clausentech.com/lchs/dclausen/algebra2/formulas/Ch12/Chapter12Formulas.htm

Check this out for more clarification on the Law of Sines and see an example of the Law of Sines.

Also, learn more about the Law of Sines and the different solutions: two solutions, one solution, or no solutions. Click here!


4. Area of an oblique triangle

According to Mrs. Kirch, "the are of an oblique (all sides different lengths) triangle is one-half of the product of two sides and the sine of their included angle."

http://www.compuhigh.com/demo/triglesson07.html

Similar to the Law of Sines, we can draw a perpendicular line "h" to make the triangle into an oblique triangle. You may know that the formula for a triangle if A=1/2bh where b represents the b and h is the height.
Based on the triangle above and concept 1, we know that Sin A= h/c and Sin B=h/c and Sin C=h/a.
When we multiply the denominators, we get cSinA=h or aSin C=h. Since we already know "h" then we can easily plug them into the original area formula of A=1/2bh. In other words, we leave the equation as is and substitute "h" for cSinA, cSinB, and bSinC

When you do this, we get:
A= 1/2 b(cSinA)                       A= 1/2 a( cSinB)                       A=1/2a (bSincC)


References:
http://www.youtube.com/watch?v=bDPRWJdVzfs
http://www.lessonpaths.com/learn/i/unit-p-supplementary-resources-and-help/ambiguous-case
http://www.compuhigh.com/demo/triglesson07.html
http://htmartin.myweb.uga.edu/6190/quickreview3a.html

WPP#12: Unit O Concept 10: Solving Angles of Elevation and Depression Word Problems

Directions: Read the word problem and answer the question.Show all work and steps clearly.

This picture will go over the solution to this word problem.Make sure to try it on your own first before looking at this picture.


Part A:
Scott went to San Francisco to sight see what his friends called the best city in the world! Of course, he wanted to intake the beauty of the city by standing from one of the great buildings. He was approximately 45 ft. from one of the buildings. He measured the elevation to the building to be 25 degrees. He wanted to know how many feet above the ground his view would be. How tall was the building?



Note:  "X" is the missing side that we need, the height of the building (also the opposite side). The distance between Scott and the building is 45 ft, which is adjacent to the angle (elevation). Remember to use tan and not the inverse since we are not looking for an angle, but a side instead.

Part B:
Once he was at the top of the building, he spotted his best friend Anna who happened to be at the ice cream shop eating ice cream. Suddenly, he got a crave for ice cream and wanted to accompany her. The angle of depression from the top of the building to Anna was 29 degrees. How far apart was the building that Scott was standing on to the ice cream shop that Anna was at? (Hint: Use "Part A" to find the length of the building. This will help you complete the ratio.)


Note: Since we referred back to the previous part and found out that "x" (height) was 20.98 ft. we can make that the adjacent side to the ratio. The missing distance between both building is represented by the variable "x", which also tangent. Again, we only use tan and not the inverse since we are only looking for the distance and not the angle.

I/D #2: Unit O - How can we derive the patterns for our special rights triangle?

HEADING FOR THIS SECTION: INQUIRY ACTIVITY SUMMARY Please click here to watch video


HEADING FOR THIS SECTION: INQUIRY ACTIVITY REFLECTION

Something I never noticed before about special right triangles is how they all connect one way or another. I knew that triangles all add up to 180 degrees, but I had forgotten that if you divide the triangle by half, you get a right triangle and then a 30-60-90. Of course, the 45-45-90 also derives from another shape, but this time it is the square. I never noticed that the triangle is simply a ratio that will always remain the same even as the triangles expand.

Being able to derive these patterns myself aids in my learning because I can always rewrite the pattern in case I happen to forget. It would only really take me knowing the Pythagorean theorem, which I hope to never forget. Finding out the pattern is actually really simple and now I have the ability to easily figure it out simply by finding the angles measurements of a triangle and not by memorizing the sides, but by actually understanding the factors of triangles.

I/D #1: Unit N Concept 7: How do SRTs and the UC relate?

Inquiry Activity Summary:

Please click here to watch the video

Inquiry Activity Reflection:

1. The coolest thing I learned from this activity was how to base my answers from one single quadrant with the three different right angles. In geometry, I would have never thought that I would see the special right triangles as much as I do now, but I am glad that I remembered them.
2. This activity will help me in this unit because I know that I am bound to forget the circle if I am ever nervous or simply cannot remember, so this activity will really help me get one quadrant organized and thus, the entire unit circle. It also allowed me to see the relationships that the degrees have with their sides and how the sides related to the circle as a whole.
3. Something I never realized before about special right triangles and the unit circle is how it always has the same numbers even though it seems to be a lot more. The amazing thing is that thiese numbers relate to the special right angle triangles, so it is easy to figure out what numbers are needed.

RWA #1: Unit M Concepts 4-6: Conic Sections in real life.

1. Definition of an ellipse:

"The set of all points such that the sum of the distance from the two points is a constant."

                                                                                                 -Mrs. Kirch
.

2.         The image above provides the equation to an ellipse. An ellipse will be horizontal (fat) or vertical (skinny) based on the bigger denominator. The left ellipse will be "fat" because the bigger number lies under the x^2 denominator; meanwhile, the right ellipse is "skinny" since the bigger denominator is under the y^2. Their order does not necessarily matter; instead, the graph is based on the bigger denominator. The main kepy points to find for an ellipse would be center, foci, major axis, minor axis, vertices, co-vertices, and eccentricity. 

http://www.teacherschoice.com.au/images/ellipse_types.gif

           If you are given the standard equation, all you have to do is complete the square before you can continue solving the puzzle. Remember, the standard form has to equal to 1 and must be added (just as the algebraic equation above shows). X always goes with "h" and Y always goes with "k", so base the center on the given equation. For example, if the equation was (x-2)^2/25 + (y+2)^2/64=1, then the center would simply be (2,-2). Given this information, you would know that the "y" has the bigger denominator and when graphed, the major axis would be x=2 and that only means the minor axis will be the other value, which will be y=-2. When these two lines are graphed, the major will be a solid line perpendicular to the dotted minor line. To find the vertices and co-vertices, keep in mind that the numbers will repeat based on the major and minor axis. In this case, x=2 for the major axis, the vertices will be (2, #) and (2, #). Given that the center, the vertices, and the foci all have the similar repeating value, you can fill in the foci as (2, #) and (2, #). Go back the co-vertices and since it is based on the minor axis, you know that the repeating number will be (#, -2) and (#, -2). The "a" and "b" values help determine the remaining values for the vertices and co-vertices points. The "a" and "b" are the square roots from the the starndard equation. To find the foci, use the equation a^2-b^2=c^2. Since most of the key points are based on the center, add the foci to the center, or the missing (non-repeating) value. You can find the eccentricity by dividing c over a. Since it's an ellipse, the eccentricity should be between 0 and 1.

http://www.mathwarehouse.com/ellipse/images/eccentricity_of_ellipse.gif

Take a look at the graph from this website to get an idea about an ellipse's eccentricity:
Click Here!

Notice how the picture on the left has an eccentricity of .8 (less than 1, yet close)

           When graphing an ellipse, remember which lines are solid vs. which ones are dotted (see previous paragraph). Also, the vertices and the co-vertices will be perpendicula to each other and both will meet at the center. The vertices should be equidistant from the center on both sides and so should the co-vertices. The foci help determine the shape of the ellipse and are fairly close to the vertices. In fact, the closer the foci are to each other, the more circular the ellipse will be (vice versa). 

http://t0.gstatic.com/images?q=tbn:ANd9GcScIq5UAbf3gnoaNjUdn5xmD4DCdO4eFKoo21Npaa6hTStyqLocWw:decodedpregnancy.com/assets/A03_Conic_Sections.jpg

                                              

Want to know more about conics? Check this out!

3. Real World Application:

http://cse.ssl.berkeley.edu/SegwayEd/lessons/cometstale/frame_orbits.html

Ellipses are mostly since in our very own solar system and all around us, of course. The comets, planets, and moons all orbit the sun through their very own ellipse shape. As you can see, those closer to the sun have smaller ellipses; meanwhile, those farter apart have a bigger ellipse. "Because the Sun is at the focus, not the center, of the ellipse, the planet moves closer to and further away from the Sun every orbit" (http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html)

http://i1.ytimg.com/vi/VjQZ5QA-tNg/hqdefault.jpg

            "Ellipsoids (three-dimensional ellipses) are used in health care to avoid surgery in the treatment of kidney stones." (http://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.424511.html) The use of ellipses in these surgery is due to the fact that ellipses have a reflective property in which one shock wave from focus point will pass through the second focus point. With the use of lithotripter, doctors have been able to get rid of kidney stones in one's body. 

http://mathcentral.uregina.ca/beyond/articles/Lithotripsy/lithotripsy1.html

  A patient will be placed right before the machine at the precise distance from the focus point and the shock wave generator. Notice how the picture on the right shows the kidney stones in one focus point while the other focus point will be at the shock. A cushion surrounds the ellipsoid, so that the water within in provides a safe transmission between the shock waves that pass through one's body. In other words, the waves that generate from one focus point to the other focus point, which would be the kidney stone. The stones then shatter and it is easy for a patient to get rid of the stones without the need for surgery, but also achieves without much risks. 

4. Works Cited:

• http://www.teacherschoice.com.au/ellipse_tool.htm
• http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html
• http://cse.ssl.berkeley.edu/SegwayEd/lessons/cometstale/frame_orbits.html
• http://www.youtube.com/watch?v=lvAYFUIEpFI
• http://mathcentral.uregina.ca/beyond/articles/Lithotripsy/lithotripsy1.html
• http://www.algebra.com/algebra/homework/Quadratic-relations-and-conic-sections/Quadratic-relations-and-conic-sections.faq.question.424511.html