 |
| http://htmartin.myweb.uga.edu/6190/quickreview3a.html |
1. The Law of Sines AAS or ASA
When we use trig function, we usually use them only with right triangles. All we have to remember if SOH -CAH- TOA or the Pythagorean Theorem. What if it is not a right triangle? Well, we can still use the trig function, to determine the Law of Sines. This way we can determine for non-right triangles.
Here it how we derive the Law of Sines:
 |
| Add cahttp://www.mathamazement.com/Lessons/Pre-Calculus/06_Additional-Topics-in-Trigonometry/law-of-sines.htmlption |
This is a non-right triangle, but we can simply make it a right triangle by drawing a perpendicular line from <B. Now we have two right triangles that we can work with.
 |
| http://www.mathamazement.com/Lessons/Pre-Calculus/06_Additional-Topics-in-Trigonometry/law-of-sines.html |
When we drew the perpendicular line, we got two right triangles. The perpendicular line can be called "h". Let's look at the relationships that the sides and angles have based on the trig function. When we do this we could get SinA=h/a and SinC=h/a (opposite.adjacent). Both equations have fractions, so to get ride of the fractions, we can , multiply by the denominator. Once we do that we get cSin A=h and aSin C=h. Since both equal "h" we can use the transitive property to get c Sin A= a Sin C. Lastly, divide both sides by "ac" to cancel off the c in one equation and a in the other.
Now we have Sin A/a= Sin C/c. However, the equation also includes SinB/b. Why don't we have it. Well, that's because we cut <B with a perpendicular. However, if we can drawn the perpendicular line from another angle, such as <A, then we could get Sin B/b.
We follow the same process and we get Sin C= h/b and Sin B=h/c. Use the transitive property and divide by "bc" and we can also get Sin B=b. Let's put it all together and we get.
We follow the same process and we get Sin C= h/b and Sin B=h/c. Use the transitive property and divide by "bc" and we can also get Sin B=b. Let's put it all together and we get.
Check this out for more clarification on the Law of Sines and see an example of the Law of Sines.
Also, learn more about the Law of Sines and the different solutions: two solutions, one solution, or no solutions. Click here!
4. Area of an oblique triangle
According to Mrs. Kirch, "the are of an oblique (all sides different lengths) triangle is one-half of the product of two sides and the sine of their included angle."
 |
| http://www.compuhigh.com/demo/triglesson07.html |
Similar to the Law of Sines, we can draw a perpendicular line "h" to make the triangle into an oblique triangle. You may know that the formula for a triangle if A=1/2bh where b represents the b and h is the height.
Based on the triangle above and concept 1, we know that Sin A= h/c and Sin B=h/c and Sin C=h/a.
When we multiply the denominators, we get cSinA=h or aSin C=h. Since we already know "h" then we can easily plug them into the original area formula of A=1/2bh. In other words, we leave the equation as is and substitute "h" for cSinA, cSinB, and bSinC
When you do this, we get:
A= 1/2 b(cSinA) A= 1/2 a( cSinB) A=1/2a (bSincC)
References:
http://www.youtube.com/watch?v=bDPRWJdVzfs
http://www.lessonpaths.com/learn/i/unit-p-supplementary-resources-and-help/ambiguous-case
http://www.compuhigh.com/demo/triglesson07.html
http://htmartin.myweb.uga.edu/6190/quickreview3a.html
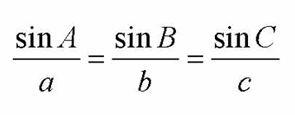
No comments:
Post a Comment